9. Traits

Methods

In Chapter 8, while studying mutable data structures, we discussed the need for providing a default value when constructing the array for implementing a generic circular queue.

fn make[T]() -> Queue[T] {
  { array: Array::make(5, T::default()), start: 0, end: 0, length: 0 }
}

In fact, we have already encountered a similar situation in Chapter 6. When implementing a generic binary search tree, we need a comparison function to determine the order of values. As illustrated in the code below, we can pass the comparison function as a parameter. While this approach is effective, it can become cumbersome when dealing with more intricate type requirements.

enum Tree[T] {
  Empty
  Node(T, Tree[T], Tree[T])
}

// We need a comparison function to determine the order of values
// -1: less than; 0: equal to; 1: greater than
fn insert[T](self: Tree[T], value: T, compare: (T, T) -> Int) -> Tree[T]
fn delete[T](self: Tree[T], value: T, compare: (T, T) -> Int) -> Tree[T]

The above examples share a common characteristic, that is, the functions are associated with the type T. For instance, we might require the following functions for T:

• Compare two T values: fn T::compare(self: T, other: T) -> Int
• Get the default value of T: fn T::default() -> T
• Get the string representation of a T value: fn T::to_string(self: T) -> String
• ...

Such functions are called the methods of T.

Traits

In MoonBit, a trait declare a list of methods to be supplied if a type wants to implement it. When defining a method's signature, we can use Self to refer to the type itself. For example,

trait Compare {
  compare(Self, Self) -> Int
}
trait Default {
  default() -> Self
}

The trait system in MoonBit is structural. That is, there is no need to implement a trait explicitly, and types with the required methods automatically implements a trait.

Bounded Generics

In generic functions, we use traits as bounds to specify what methods a type supports. In MoonBit, <type>: <trait> requires <type> to be bound by <trait>. Inside the function body, the methods of a trait can then be called via <type>::<method>(). In this way, we can rewrite the make method of type Queue as follows:

fn make[T: Default]() -> Queue[T] { // `T` should support the `default` method.
  {
    array: Array::make(5, T::default()), // The return type of `default` is `T`.
    start: 0,  end: 0,  length: 0
  }
}

With bounds, we can timely detect errors caused by calling missing methods. In the following example, we are trying to build a queue of BoxedInt, which however, does not support the default method. Consequently, the compiler notifies us of this error.

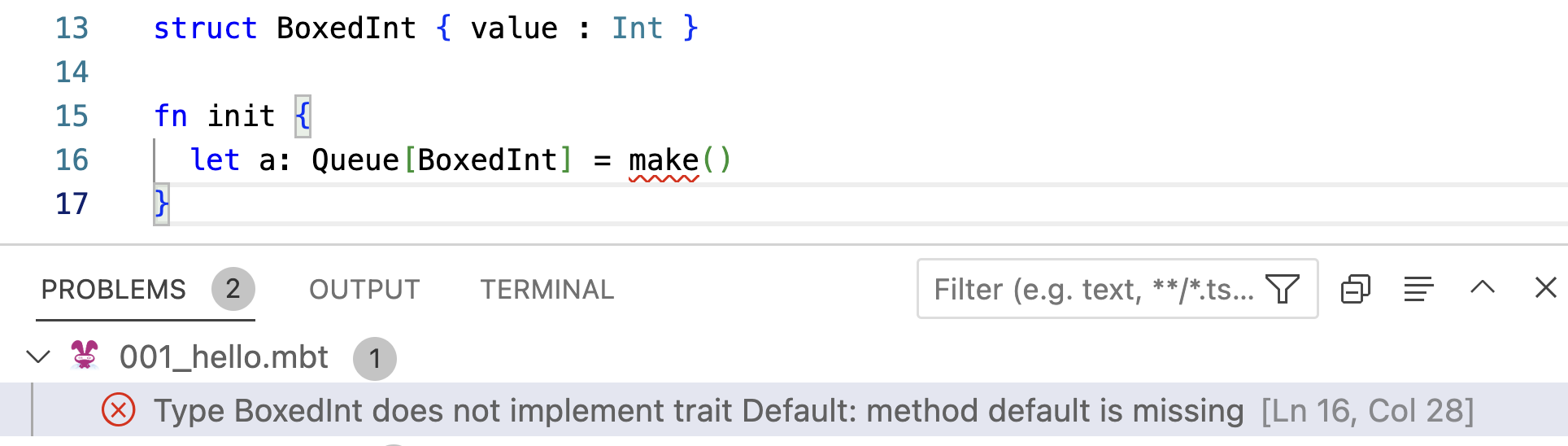
Using the same approach, we can reimplement the insert method for Tree. In particular, we need to demand that the type parameter T is bound by Compare. This enables us to compare two T values by calling T::compare directly, without requiring an additional parameter. The compare method must have been provided by T, as it is bound by Compare.

fn insert[T : Compare](tree : Tree[T], value : T) -> Tree[T] {
  // Since `T` is bound by `Compare`, it should support the `compare` method.
  match tree {
    Empty => Node(value, Empty, Empty)
    Node(v, left, right) =>
      if T::compare(value, v) == 0 { // We can call `compare` here.
        tree
      } else if T::compare(value, v) < 0 { // We can call `compare` here.
        Node(v, insert(left, value), right)
      } else {
        Node(v, left, insert(right, value))
      }
  }
}

Implementation of Traits

Implicit Implementation

Since the trait system of MoonBit is structured, to implement a trait, all we need to do is to define the corresponding methods using the syntax fn <type>::<method>(...) -> ....

In the following example, we define the default method for the BoxedInt type.

struct BoxedInt { value : Int }

fn BoxedInt::default() -> BoxedInt {
  { value : Int::default() }
  // The default value can be defined by boxing the default value of `Int`.
}

By defining the default method, the Default trait is now implemented. Therefore, we can construct a queue of BoxedInt using the make function, which internally invokes the default method of BoxedInt.

fn init {
  let array: Queue[BoxedInt] = make()
}

Explicit Implementation

Alternatively, we can implement a trait explicitly with the following syntax:

// Provide a default implementation for method `method` of trait `Trait`
impl Trait with method(...) { ... }

// Implement method method of trait `Trait` for type `Type`
impl Trait for Type with method(...) { ... }

// With type parameters
impl[X] Trait for Array[X] with method(...) { ... }

Compared to the previous syntax fn Trait::method(...), the new syntax allows explicit specification of the implementing type, providing richer and clearer signature information. Since the type is specified, the compiler can automatically infer the method's parameter and return types, eliminating the need for manual annotations:

trait MyTrait {
  f(Self) -> Option[Int]
}

// No need to annotate `self` and the return type
impl MyTrait for Int with f(self) {
  // Compiler can automatically infer that the return type is `Option[Int]`
  Some(self)
}

Automatic Derivation

In MoonBit, it is possible to automatically derive certain basic traits by adding derive(<traits>) after the type declaration. If the type is composed of other types, those member types must have already implemented the same traits.

In the given example, we derive the Default, Eq, Compare, and Debug traits for BoxedInt. These traits can be successfully derived because Int already implements them. However, if the required traits are not implemented by the member types, the compiler will generate an error message.

struct BoxedInt { value : Int } derive(Default, Eq, Compare, Debug)

Method Chaining

In addition to <type>::<method>(<expr>, ...), we can as well call the method using <expr>.<method>(...), given <expr> is of type <type>. When defining such methods, <type>:: can also be omitted when the first parameter is named self.

In this way, when we need to call such functions sequentially, we can avoid multiple nesting of method calls, thereby enhancing the readability of the code.

fn BoxedInt::plus_one(b: BoxedInt) -> BoxedInt {
  { value : b.value + 1 }
}
// `<type>::` can be omitted when the first parameter is named `self`.
fn plus_two(self: BoxedInt) -> BoxedInt {
  { value : self.value + 2}
}

fn init {
  let _five = { value: 1 }.plus_one().plus_one().plus_two()
  // This avoids multiple nesting of method calls.
  let _five = plus_two(plus_one(plus_one({value: 1})))
}

Example: Using Traits to Implement a Map

Now, let's proceed to implement a generic map using traits.

A map is a collection of key-value pairs, where each key is associated with a value. It is possible for different keys to correspond to the same value. For instance, in the map { 0 -> "a", 5 -> "Hello", 7 -> "a"}, the key 5 corresponds to the value "Hello", while both keys 0 and 7 correspond to the value "a".

type MyMap[Key, Value]

A map should support the following methods:

• Create a map.

  fn make[Key, Value]() -> MyMap[Key, Value]
  

• Add a key-value pair, or update the corresponding value of a key.

  fn put[Key, Value](map: MyMap[Key, Value], key: Key, value: Value) -> MyMap[Key, Value]
  

• Get the corresponding value of a key.

  fn get[Key, Value](map: MyMap[Key, Value], key: Key) -> Option[Value]
  

  Since such a key-value pair may not exist in the map, the return value is wrapped in Option.

The map can be implemented using a list of pairs.

type MyMap[Key, Value] @immut/list.T[(Key, Value)]

The first two basic methods, make and put, can be easily implemented as follows:

• Create a map by creating an empty list.

  fn make[Key, Value]() -> MyMap[Key, Value] {
    MyMap(Nil)
  }
  

• Add/update a key-value pair by inserting the pair to the beginning of the list.

  fn put[Key, Value](map: MyMap[Key, Value], key: Key, value: Value) -> MyMap[Key, Value] {
    let MyMap(original_map) = map
    MyMap( Cons( (key, value), original_map ) )
  }
  

The third method, get, is also easy to describe in prose:

• Search the list from the beginning until the first matching key is found.

In such an implementation of the get function, we need to compare the key we are searching for with the keys stored in the map to determine if they are equal. As a result, the Key type must implement the Eq trait. That is, we need to modify the previous declaration of get so that Key is bound by Eq.

The complete implementation of get is as follows:

fn get[Key: Eq, Value](map : MyMap[Key, Value], key : Key) -> Option[Value] {
  loop map.0 {
    Nil => None
    Cons((k, v), tl) => if k == key {
      // `Key` is bound by `Eq`, so we can call `==` directly.
      Some(v)
    } else {
      continue tl
    }
  }
}

In the above implementation, we loop through the list and use the == operator to determine whether the current key matches the one we are looking for. It can be shown that when there are multiple identical keys, we will always retrieve the latest value associated with that key.

Custom Operators

In MoonBit, operators can be customized by defining methods with specific names and types. For instance, by defining the op_equal and op_add methods, we can use the == operator to compare two BoxedInt values and use the + operator to add two BoxedInt values.

fn BoxedInt::op_equal(i: BoxedInt, j: BoxedInt) -> Bool {
  i.value == j.value
}
fn BoxedInt::op_add(i: BoxedInt, j: BoxedInt) -> BoxedInt {
  { value: i.value + j.value }
}

fn init {
  let _ = { value: 10 } == { value: 100 } // false
  let _ = { value: 10 } + { value: 100 } // { value: 110 }
}

In the previous example, we used the get and set functions to access and update data in the map. However, it is also possible to use custom operators to achieve the same functionality. By defining the op_get and op_set methods for the MyMap type, we can use the map[k] syntax to retrieve the value corresponding to k, and use map[k] = v to update the value associated with k to v.

fn MyMap::op_get[Key: Eq, Value](map: MyMap[Key, Value], key: Key) -> Option[Value] {
  get(map, key)
}
fn MyMap::op_set[Key: Eq, Value](map: MyMap[Key, Value], key: Key, value: Value) -> MyMap[Key, Value] {
  put(map, key, value)
}

fn init {
  let empty: MyMap[Int, Int] = make()
  let one = { empty[1] = 1 } // let one = MyMap::op_set(empty, 1, 1)
  let _ = one[1] // let _ = MyMap::op_get(one, 1)
}

In the previous example, the assignment statement is essentially an expression, and the return value is determined by the op_get method. We can use this method to retrieve the updated value. For mutable data structures, we also have the option to modify them in place without returning any value.

With the implementation of op_get, we can introduce pattern matching support to MyMap. This feature is applicable when the key is a native type and the value is an Option[T].

fn init {
  let empty : MyMap[Int, Int] = make()
  let one = {
    empty[1] = 1
  }
  match one {
    { 2? : Some(y) } => println(y)
    { 2? : None, 1? : Some(k) } => println(k)
    { 2? : None, 1? : None } => println("empty")
  }
}

When matching, it is important to note that the key needs to be a literal value. In { "key"?: pat }, the type of the pattern pat should be Option[T]. It is worth mentioning that the key-value pair pattern is open, meaning that any unmatched keys will be ignored even if they exist. Additionally, the code generated for key-value pair patterns is optimized, ensuring that each key is only queried at most once.

Summary

In this chapter, we learned how to

• Define traits and use them to bound type parameters
• Implement traits implicitly or explicitly
• Implement custom operators
• Implement a simple map using traits in MoonBit